Orders of Growth

Order	Linear	Polynomial	Exponential	Factorial
Example	$n$	$n^2$, $n^3$	$2^n$, $e^n$, $10^n$	$n!$, $n^n$
$n = 1000$	$10^3$	$10^6$, $10^9$

Exercise:
For each of the following pairs of functions, indicate which one has a higher order of growth.

1. $n(n+1)$ and $2000n^2$
   • $\approx$ same -- within constant multiple
2. $100n^2$ and $0.01n^3$
   • cubic has higher order of growth than quadratic
3. $\log_2 n$ and $\ln n$
   • All logarithmic functions have $\approx$ same growth within const multiple (can change log's base by the formula $\log_a n = \log_a b \log_b n$)
4. $log_2^2 n$ and $log_2 n ^2$
   • $\log_2^2 n = \log_2n \log_2n$ and $\log_2 n^2 = 2 \log_2 n$
5. $2^{n-1}$ and $2^n$
   • $2^{n-1} = \frac{1}{2} 2^n$ so $\approx$ same order of growth as $2^n$
6. $(n-1)!$ and $n!$
   • $(n-1)!$ has lower order of growth since $n! = n(n-1)!$

Analysis of Non-Recursive Algorithms

Example 1:

Max Element
Input: an array, A
Output: the largest element in A

maxVal <- A[0]
for i <- 1 ... A.length-1
  if A[i] > maxVal
    maxVal <- A[i]
return maxVal

What is the input size? (A.length)
What is the basic operation? (Comparison)
What do we expect its complexity class to be? (Linear)

$C(n) = \sum_{i=1}^{n-1} 1$
$= (n - 1) - 1 + 1$ (from previous formula)
$= (n - 1) \in \Theta(n)$

---

Example 2:

Bubble Sort
Input: an array, A of sortable elements
Output: a permutation of A in non-decreasing order

for i <- 0 ... A.length - 2
  for j <- 0 ... A.length - 2 - i
    if A[j+1] < A[j]
      swap A[j] and A[j+1]
return A

What's the input size? n = A.length
Basic operation? Swap
What do we expect its complexity class to be? Polynomial

$C(n) = \sum_{i=0}^{n-2} \sum_{j=0}^{n-2-i} 1$
$= \sum_{i=0}^{n-2} n-1-i$ (the inner cycles happen n - i - 1 times)
$= \sum_{i=1}^{n-1} i$
$= \frac{n(n-1)}{2} \in \Theta(n^2)$

---

Example 3:

Matrix Summation

Input: a $w \times h$ matrix, M
Output: The sum of all elements in M

total <- 0
for i <- 0 ... w - 1
  for j <- - ... h - 1
    total <- total + M[i][j]
return total

Input size? $w \cdot h$
Basic operation? Addition
Expected complexity class? Linear

$C(n) = \sum_{i=0}^{w-1} \sum_{j=0}^{h-1} 1$
$= \sum_{i=0}^{w-1} h$
$= h \sum_{i=0}^{w-1} 1$
$= h \cdot w$ $= n \in \Theta(n)$

---

Example 4:

---

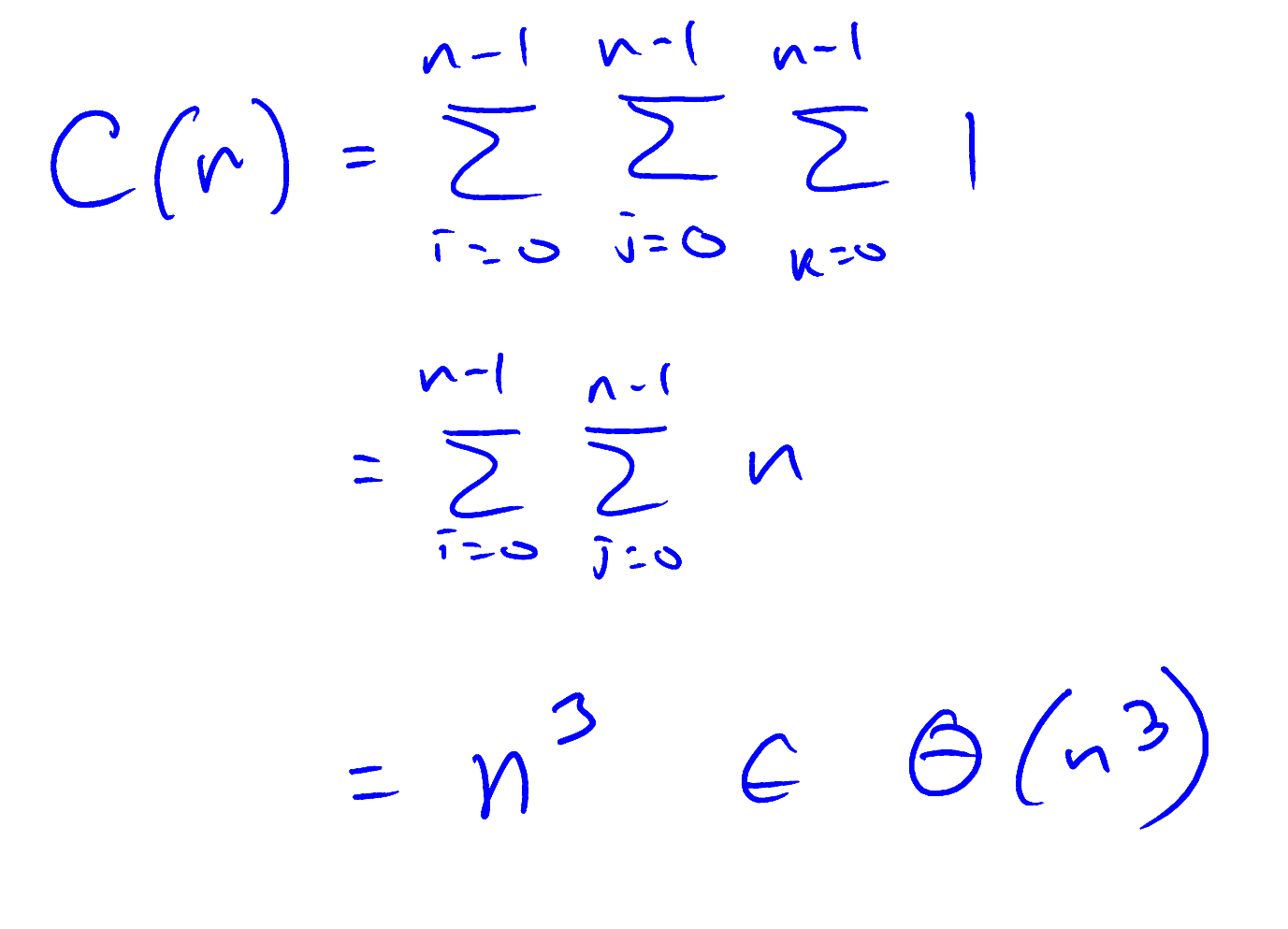
Example 5: