http://imgs.xkcd.com/comics/efficiency.png
Summation Review
Proof:
Proof:
a_n - {a_{n-1}}
{a_{n-1}} - {a_{n-2}}
...
a_1 - a_0
General: where
Important Problem Types
- Sorting
- Searching
- String Processing
- Graph Problems
- Combinatorial Problems
- Geometric Problems
- Numerical Problems
Important Design/Problem Solving Techniques
- Brute Force/Exhaustive
- Greedy
- Divide and Conquer
- Decrease and Conquer
- Transform and Conquer
- Space and Time Tradeoff
- Dynamic Programming
- Iterative Improvement
- Backtracking
- Branch and Bound
Fundamental Data Structures
- List
- Array
- Linked List
- String
- Stack
- Queue
- Priority Queue/Heap
- Graph
- Tree
- Set
- Dictionary
The Analysis Framework
Issues:
-
Correctness
-
Time Efficiency and Space Efficiency
- Time efficiency (also called time complexity) is a measure of how fast an algorithm in question runs.
- Space efficiency (also called space complexity) is a measure of the amount of extra memory required by the algorithm in addition to the space needed for its input and output.
-
Optimality
Approaches
-
Theoretical Analysis (with math)
- Time efficiency is analyzed by determining the number of repetitions of the basic operation as a function of input size
- Basic operation: the operation that contributes most toward the running time of the algorithm
where is the running time
is the input size
is the execution time for the basic operation
and is the number of times basic operation is executed.- Examples:
Problem Input Size Basic Op Searching for key in a list of items Number of list's items Key comparison Multiplication of two matrices matrix dimensions or total number of elements Multiplication of two numbers Checking primality of a given integer 's size = number of digits (say in binary representation) Division Typical graph problem Number of nodes and/or edges Visiting a node or traversing an edge - Time efficiency is analyzed by determining the number of repetitions of the basic operation as a function of input size
-
Empirical Analysis
- Select a specific (typical) sample of inputs
- Use physical unit of time (e.g. milliseconds) or count actual number of basic operation executions
- Analyze the empirical data
-
For some algorithms, efficiency depends on input form
- Worst case - = maximum over inputs of size
- Best case - = minimum over inputs of size
- Average case - = "average" over inputs of size
- Number of times the basic operation will be executed on typical input
- NOT the average of worst and best case
- Expected number of basic operations is considered as a random variable under some assumption about the proability distribution of all possible inputs
Sequential Search Example
Search for a given value in an array
SequentialSearch
Input: An array, , of length and a search key
Output: The index of the first element of that matches or if there are no matching elements
i <- 0
while i < n and A[i] != K do
i <- i + 1
if i < n
return i
else
return - 1
-
Worst case:
Analyze the algorithm to see what kind of inputs yield the largest value of the basic operation's count nC_{worst}(n) = n$ if counting key comparisons. -
Best case:
-
Average case:
To analyze the algorithm's average case efficiency we must make some assumptions about possible inputs of size .
(a) Assume the probability of a successful search is equal to
(b) the probability of the first match occurring in the th position of the list is the same for everyIn the case of a successful search, the probability of the first match occurring in the th position is for every , and the number of comparisons is . In the case of unccessful match, the # of comparisons is with the probability of such a search being .
-
-
Is average case important? YES! But rarely easy to do. Probabilistic assumptions are hard to verify.
-
For most algorithms, we will simply quote already proven average case analysis
-
Asymptotic Analysis
'Big Oh'
The set of all functions with a lower or the same order of growth as
Examples:
The set of all functions with a higher or same order of growth as
The set of all functions with the same order of growth as
if is bounded above by some constant multiple of for all large .
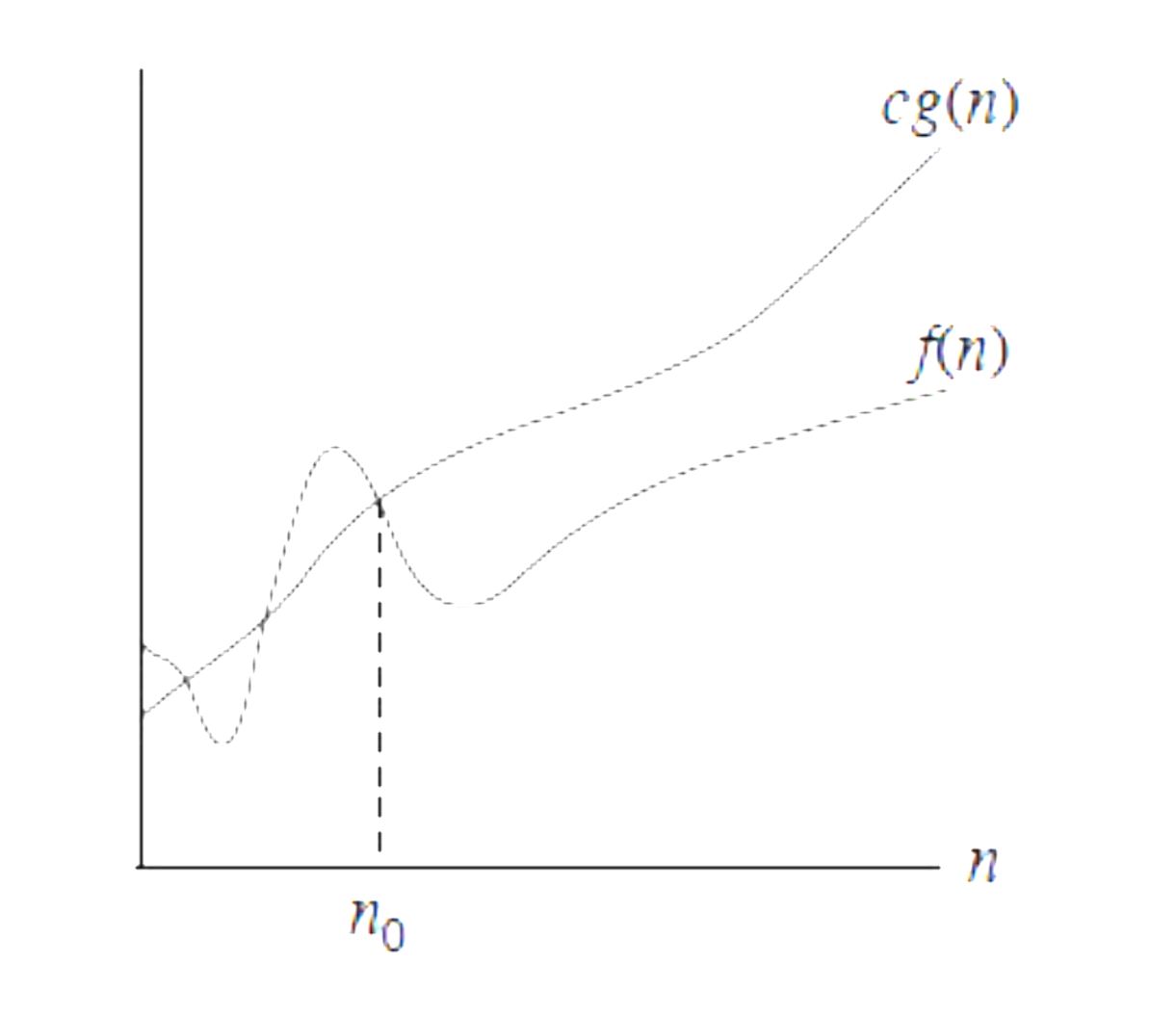
,
where and
if is bounded below by some constant multiple of for all large .
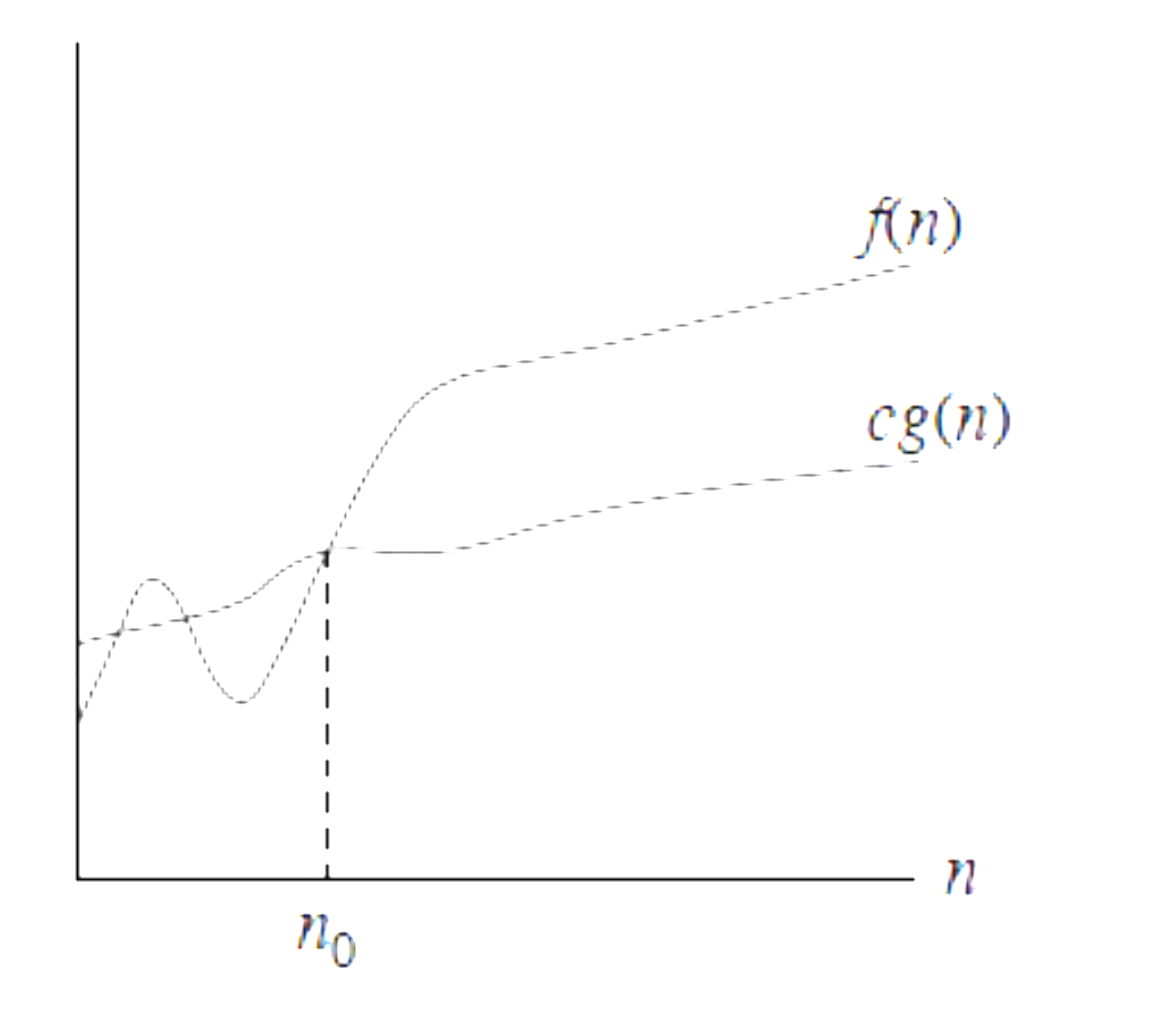
if is bounded both above and below by some constant multiple of n$
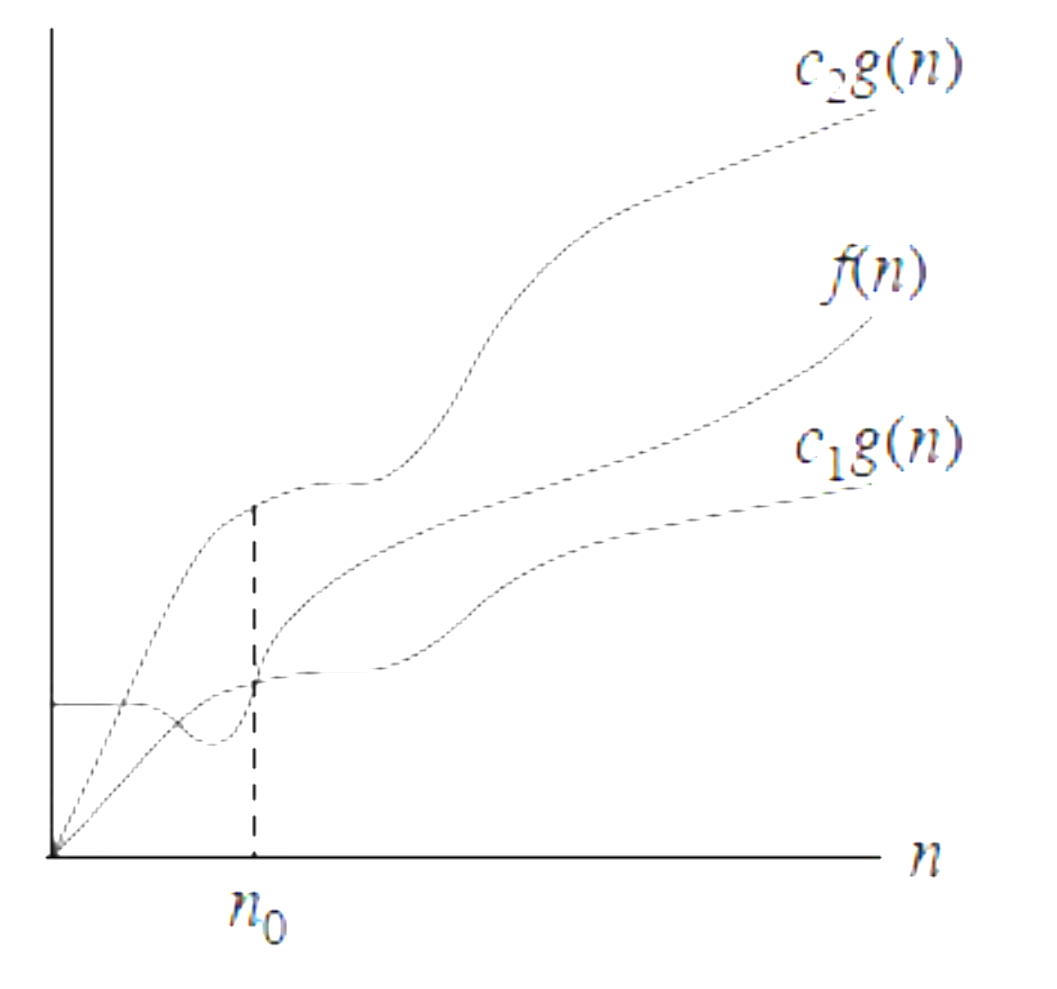
Example:
General Plan for Analysis (Nonrecursive algorithms)
- Decide on parameter indicating input size
- Identify Algorithm's basic operation
- Determine best, worst, and average cases for input size
- Set up a sum for the number of times the basic operation is executed
- Simplify the sum using standard formulas and rules (Appendix A in the textbook)
Limits?
Basic Efficiency Classes and Descriptions (p59)
Algorithm Example (if time permits)
Interval Scheduling