P vs. NP

One of the fundamental mathematics problems of modern times.

Millennium Prize Problems

1. Birch & Swinnerton-Dyer Conjecture
2. Hodge Conjecture
3. Navier-Stokes Equations
4. P vs. NP
5. Poincare Conjecture
6. Riemann Hypothesis
7. Yang-Mill Theory

P vs NP asks whether every problem whose solution can be quickly verified (technically, verified in polynomial time) can also be solved quickly (again, in polynomial time).

---

Halting Problem: Some problems can't be computed:

Unsolvable (by computer) Problem

• Suppose that you could write a program

    boolean halts(Program p, Input i);
  

that returns true if p halts on input i, and false if it doesn’t.

• Then I can write

    boolean loopIfHalts(Program p, Input i) {
    if (halts(p,i))
    while (true) ;
    else
    return true;
    }
  

which loops if p halts on input i, and true if it doesn’t

---

Prime factor

In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these integers are further restricted to prime numbers, the process is called prime factorization.

Semi-primes are the product of two primes. These are the hardest instance of the prime factorization problem.

Which is harder?

• $13 \cdot 7 = ?$
• $? \cdot ? = 91$

---

---

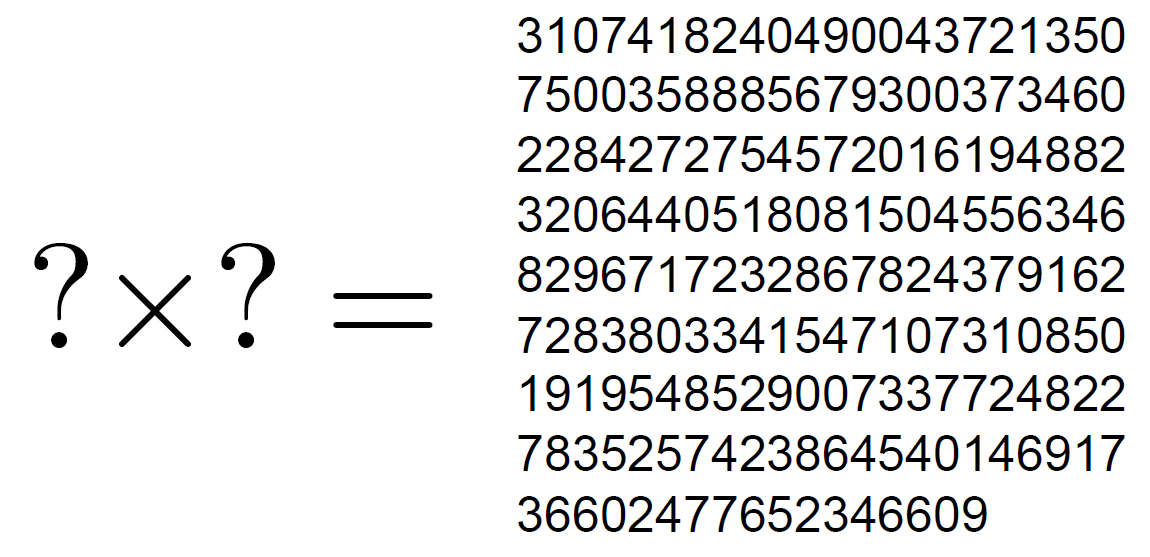
Factoring is in NP

• If given a solution we can check it quickly

---

Problem Types

• Optimization problem: find a solution that
  maximizes or minimizes some objective function
• Decision problem: answer yes/no to a question
• Many problems have decision and optimization
  versions.
  • e.g.: traveling salesman problem
  • optimization: find Hamiltonian cycle of minimum length
  • decision: find Hamiltonian cycle of length ≤ m
• Decision problems are more convenient for
  formal investigation of their complexity.

---

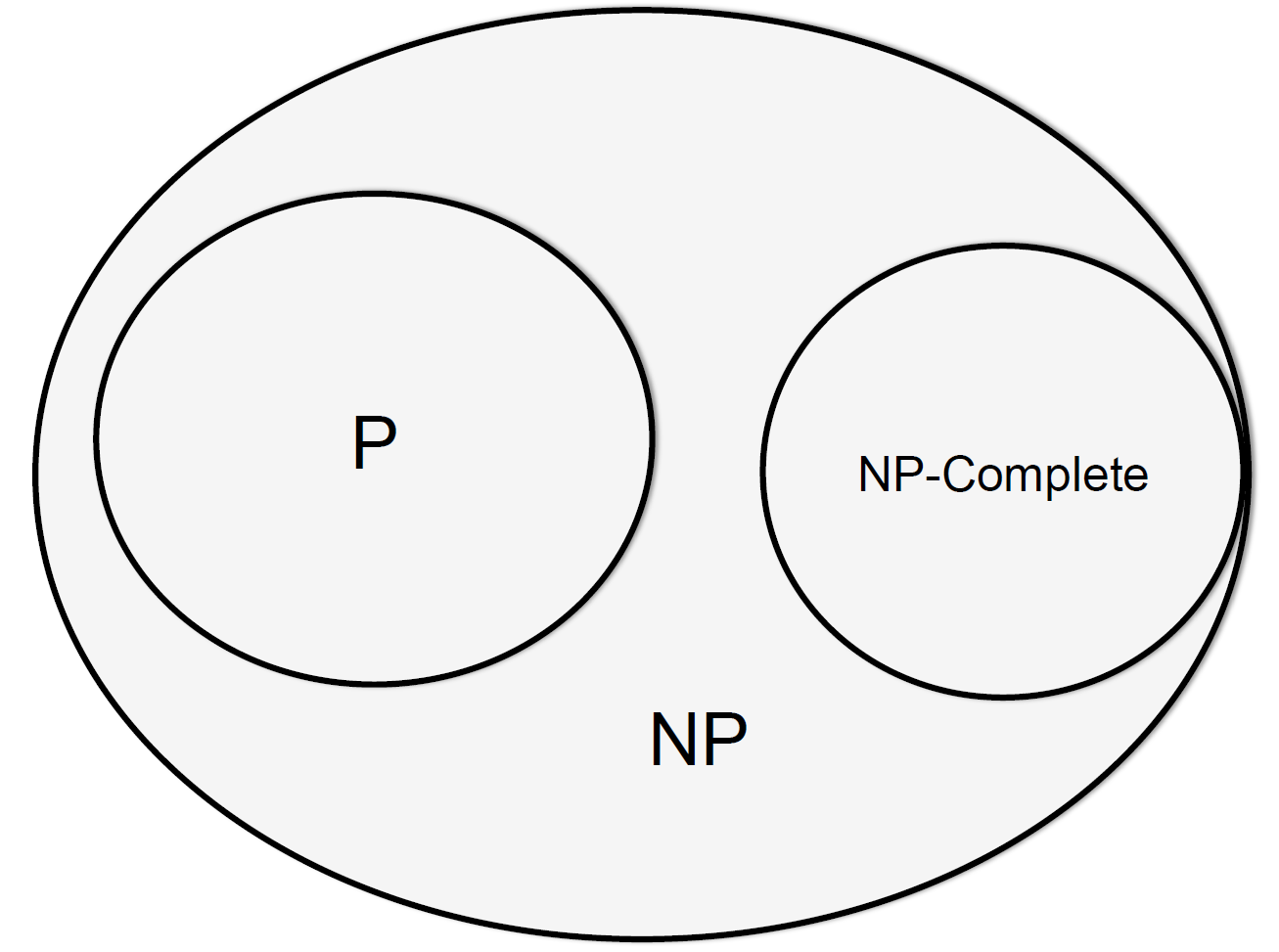
Class P

• P: the class of decision problems that are
  solvable in O(p(n)) time, where p(n) is a
  polynomial in problem’s input size n
• Examples:
  • searching
  • element uniqueness
  • graph connectivity
  • graph acyclicity
  • primality testing (finally proven in 2002)

---

Class NP

• NP (nondeterministic polynomial): class of decision
  problems whose proposed solutions can be verified in
  polynomial time = solvable by a nondeterministic
  polynomial algorithm
• A nondeterministic polynomial algorithm is an abstract twostage
  procedure that:
  1. generates a random string purported to solve the problem
  2. checks whether this solution is correct in polynomial time

By definition, it solves the problem if it’s capable of
generating and verifying a solution on one of its tries

Example: CNF satisfiability
Problem: is a boolean expression in its conjunctive normal form
(CNF) satisfiable, i.e., are there values of its variables that makes it
true?
This problem is in NP. Nondeterministic algorithm:

1. Guess truth assignment
2. Substitute the values into the CNF formula to see if it evaluates to true

Example: $(A ⋁ ¬B ⋁ ¬C) ⋀ (A ⋁ B) ⋀ (¬B ⋁ ¬D ⋁ E) ⋀ (¬D ⋁ ¬E)$

A	B	C	D	E
0	0	0	0	0
…
1	1	1	1	1

Checking phase: $\mathcal{O}(n)$

Some NP Problems
• Circuit Routing
• Travelling Salesman
• Knapsack problem
• Protein Folding
• Theorem Proving
• Crossword puzzle generation
• Sudoku

---

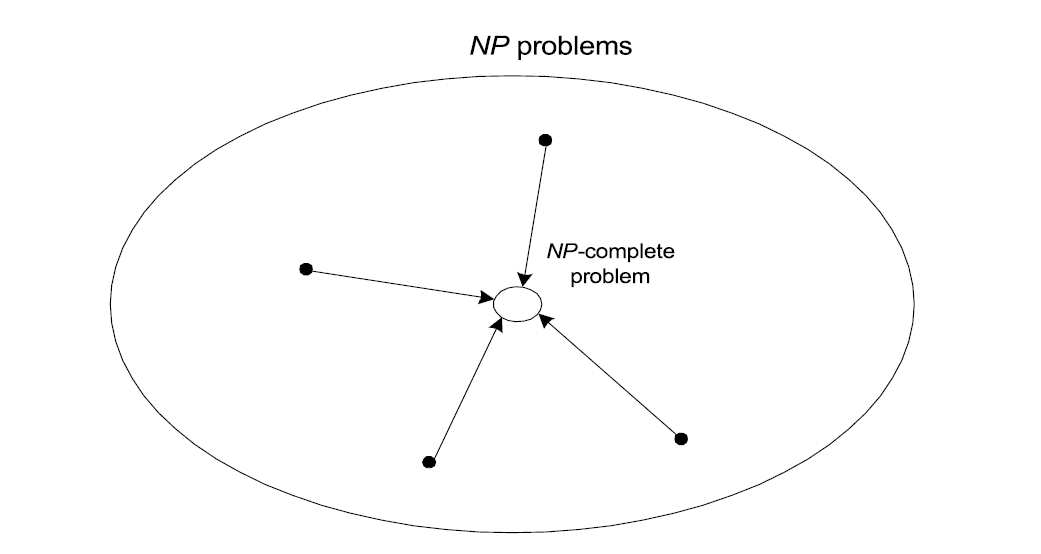
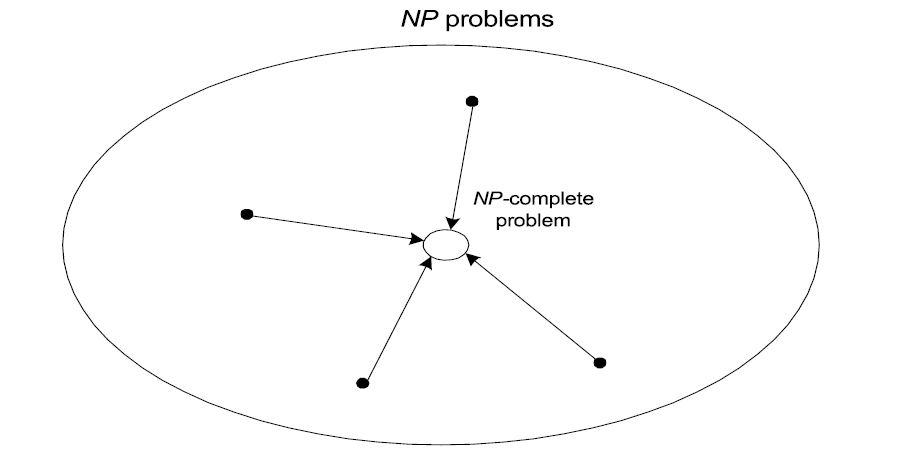
NP-Complete

A decision problem D is NP-complete if it is as hard as any
problem in NP, i.e.,

1. D is in NP
2. every problem in NP is polynomial-time reducible to D

Other NP-complete problems obtained through polynomial-time
reductions from a known NP-complete problem

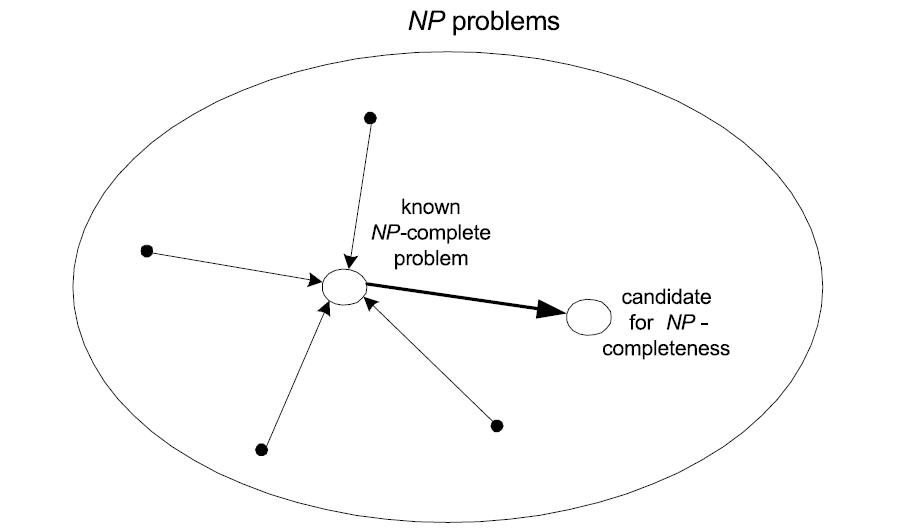
• Examples: TSP, knapsack, partition, graph-coloring and
  hundreds of other problems of combinatorial nature (with a few exceptions, such as MST and shortest path).

---

Knapsack?

• Didn’t we solve this by Dynamic
  Programming?

• For a knapsack of capacity W, and n items,
  how big is the table? n × W

• What’s the efficiency of the Dynamic
  Programming Algorithm?

  A. O(n)
  B. O(W)
  C. O(nW)
  D. O(Wn)
  E. None of
  the above
  

Complexity of Dynamic Programming
algorithm is in O(nW)

• So why is Knapsack in NP?

DEFINITION 1 We say that an algorithm solves a
problem in polynomial time if its worst-case time
efficiency belongs to O(p(n)) where p(n) is a polynomial
of the problem’s input size n. [Levitin, p. 401]

---

P = NP ?

• P = NP would imply that every problem in NP, including all NP-complete
  problems, could be solved in polynomial time
• If a polynomial-time algorithm for just one NP-complete problem is
  discovered, then every problem in NP can be solved in polynomial time,
  i.e., P = NP

• Most (but not all) researchers believe that P ≠ NP , i.e., P is a proper
  subset of NP

Computation Complexity

A whole field of study that investigates classes of problems.

Co-NP is the class of all problems where a wrong answer can be quickly rejected

PSPACE - The set of all problems that can be solved using only a polynomial amount of addition space using a deterministic algorithm

NPSPACE The - the set of all problems that can be solved using only a polynomial amount of addition space using a nondeterministic algorithm

EXP - The set of all problems solvable in exponential time

BPP - Bounded-Error Probabilistic Polynomial-Time -The class of feasible problems given a genuine random-number source

EXPSPACE - The set of all problems that can be solved using only an exponential amount of addition space