Dijkstra(G, s)
Input: A weighted connected graph G = (V, E) with nonnegative weights and a starting vertex s
Output: The length d_v of a shortest path from s to v

Q <- empty priority queue
for every vertex v in V:
  d_v <- \inf
  p_v <- null
  Insert(Q, v, d_v)   // initialize every vertex v with \inf distance
d_s <- 0  // Set the distance of the starting vertex s to be 0 (zero distance to itself)
V_r <- /emptyset  // set for which a shortest path is found
for i <- 0 ... |V|-1:
  u* <- DeleteMin(Q)    //extract minimum priority element
  V_r <- V_r \union {u*}
  for every vertex u in V - V_r that is adjacent to u*:
    if d_u* + w(u*, u) < d_u:
      d_u <- d_u* + w(u*, u)
      p_u <- u*
      Decrease(Q, u, d_u)

from Wikipedia:

1  function Dijkstra(Graph, source):
2
3      create vertex set Q
4
5      for each vertex v in Graph:             
6          dist[v] ← INFINITY                  
7          prev[v] ← UNDEFINED                 
8          add v to Q                      
10      dist[source] ← 0                        
11      
12      while Q is not empty:
13          u ← vertex in Q with min dist[u]    
14                                              
15          remove u from Q
16          
17          for each neighbor v of u:           
18              alt ← dist[u] + length(u, v)
19              if alt < dist[v]:               
20                  dist[v] ← alt
21                  prev[v] ← u
22
23      return dist[], prev[]

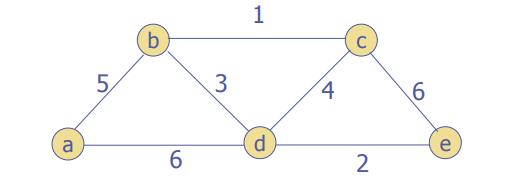
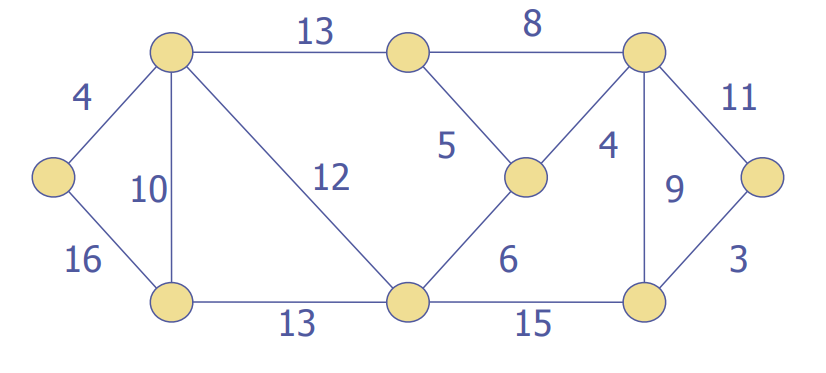
p336 and p 337 for some examples

In general the running time of Dijkstra's is given by $O(|E| \cdot T_d + |V| \cdot T_e)$.

In an implementation of Dijkstra's algorithm that reinserts nodes into the priority queue with their new priorities, one node is added to the priority queue for each of the m edges in the graph. This means that there are m enqueue operations and m dequeue operations on the priority queue, giving a total runtime of O(m Te + m Td), where Te is the time required to enqueue into the priority queue and Td is the time required to dequeue from the priority queue.

In an implementation of Dijkstra's algorithm that supports decrease-key, the priority queue holding the nodes begins with n nodes in it and on each step of the algorithm removes one node. This means that the total number of heap dequeues is n. Each node will have decrease-key called on it potentially once for each edge leading into it, so the total number of decrease-keys done is at most m. This gives a runtime of (n Te + n Td + m Tk), where Tk is the time required to call decrease-key.

Queue	T_e	T_d	T_k	w/o Dec-Key	w/Dec-Key
Array/LL	N			O(N^2)
Binary Heap	O(log N)	O(log N)	O(log N)	O(M log N)	O(M log N)
Fibonacci Heap	O(1)	O(log N)	O(1)	O(M log N)	O(M + N log N)