CS350
Lecture Notes - 1

Happy Birthday!

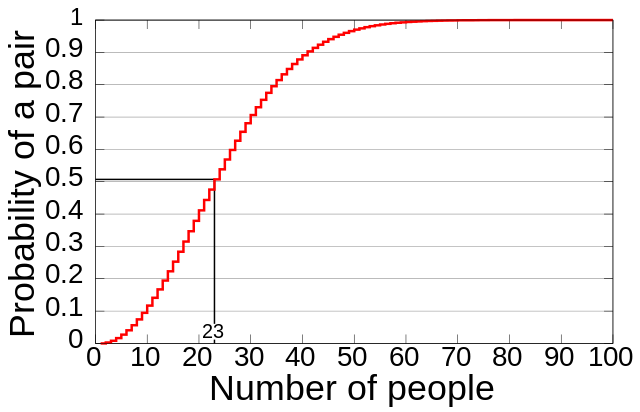
Are there two people in this room with the same birthday?

If so: what day is it?

How might we go about answering this question?

One possible algorithm:

  for each person in the room:
    find each's birthday on the calendar
      if the calendar day is marked
        return that day
      else
        mark that day
  return false

Another possible algorithm

  for each person in the room:
    write each's birthday on the whiteboard
    for other people in the room:
      if other's birthday is on the whiteboard
        return birthday
  return false

Which of these algorithms is better?

What does it mean for an algorithm to be better?
- How much effort does each one take?

Are there other algorithms that solve this problem?

Complexity:

How do we compare algorithms?
- Efficiency
  - Time
  - Space
- Simplicity
  - How to measure?
- Generality
  - How to measure?
How do we compare problems?
What are the limits of computation?

Efficient procedures for solving large scale problems

Today, one trillion is a large problem
In my college days, one million was a large problem
In your other PSU prof's days, one thousand was a large problem (few decades ago)

Scalability

Track how our algorithms perform as inputs get larger and larger

Why study algorithms?

It's required
Recognize common patterns and problem-solving strategies
Be able to analyze algorithms for efficiency
Not be constrained by programming language
Better hardware is not a solution
Strengthen mathematical, programming, and problem-solving skills
Build a repertoire of algorithmic building blocks
It's fun
Companies that are hiring care about algorithms

Administrative Details

On Syllabus:
David Lu
Office: TBA (Feng Liu's old office 120-09)
email: dlu@pdx.edu
Course webpage: https://davidjlu.github.io/CS350/
Will use D2L as a grade book, so you can access and keep track of your grades through the quarter.
TA: Neil Babson
Office Hours: Tues/Thurs 2-3PM in fishbowl
email: nbabson@pdx.edu

Go over syllabus

Look at schedule.
Schedule is tentative.

Winter weather policy!

Schedule Philosophy and Textbook

Textbook is grouped by design strategy

Pros
- Focus on design strategies
- Return to same problems multiple times over the course of the quarter
Cons
- Return to same problems multiple times over the course of the quarter
- Unnatural in real world

Group by problem type - CLRS (Algorithms Bible)

Pros
- Focus on analysis -- immediate comparison between algorithms
- Natural in the real world
Cons
- Students may not be able to keep up with design strategies

Levitin is supposed to be much more readable than CLRS

Schedule and Assessments:

Homeworks
* 4 problem sets
* 2 will feature implementing some algorithms and testing
Midterm
Final - Date?

Intro to Algorithms

"An algorithm is a sequence of unambiguous instructions for solving a problem, i.e. for obtaining a required output for any legitimate input in a finite amount of time." (Levitin 1.1)

Another Example

Find Duplicates
Input: a length n array, A, of integers.
Output: true if the array contains a duplicate and false otherwise

  for i <- 1 ... n
    for j <- 1 ... n
      if i !=j and A[i] = A[j] then
        return true
  return false

How do we know whether this algorithm correctly solves the problem for any legitimate input?

Asymptotic Analysis

Running time usually varies with input size
- How do we measure input size?
Comparisons between algorithms should be independent of hardware and programming language

Idea: Count basic operations -- the operation contributing most to the running time

Analysis - Find Duplicates
$C(n) = \sum_{i=1}^{n} \sum_{j=1}^{n} 2$

(why 2?)

$= 2 \sum_{i=1}^{n} \sum_{j=1}^{n} 1$
$= 2 \sum_{i=1}^{n} n$
$= 2n^2$

Units for measuring running time
Let $c_{op}$ be the execution time of an algorithm's basic operation, and let $C(n)$ be the number of times this operation needs to be executed for the algorithm. Then we can estimate the running time $T(n)$ of a program implementing this algorithm by the formula

$T(n) \approx c_{op}C(n)$

Less Stupid Find Duplicates
Input: a length n array, A, of integers.
Output: true if the array contains a duplicate and false otherwise

  for i <- 1...n-1
    for j <- i+1...n
      if A[i] = A[j] then
        return true

Is this a correct algorithm to solve the problem?

Analysis - Less Stupid Find Duplicates
$C(n) = \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} 1$
$= \sum_{i=1}^{n-1} n-i$
$= \sum_{i=1}^{n-1} i$
$= \frac{n(n-1)}{2}$
$= \frac{1}{2}(n^2-n)$
$\approx \frac{1}{2}n^2$

What happens if we double the input size?

$\frac{T(2n)}{T(n)} = \frac{c_{op}C(2n)}{c_{op}C(n)}$
$= \frac{\frac{1}{2}(2n)^2}{\frac{1}{2}n^2}$
$= \frac{4n^2}{n^2}$
$= 4$

About 4 times longer!

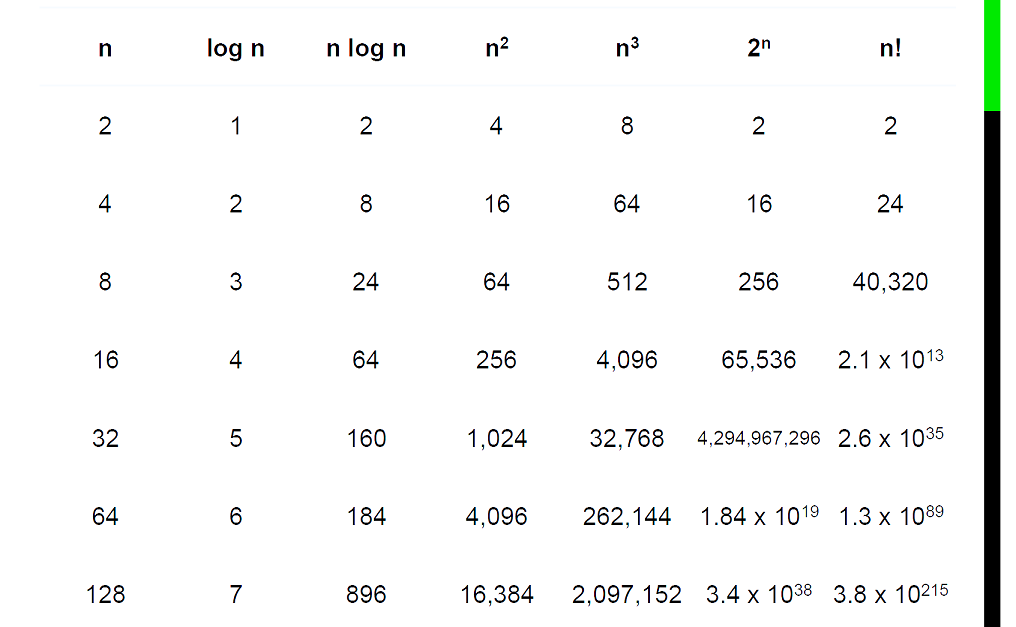
Orders of growth

Orders of growth
Also factorial
Exponential and above is HARD!
Growth

For Wed read sections 2.1 and 2.2.
I will prepare HW1 and place it in the assignments tab on the course website.