RSA Algorithm and Polynomial-Time Reduction of 3SAT to K-clique

In week 9, we saw that problems in the class P are those that can be solved easily, i.e. solved in polynomial time. We're sure there are problems that are hard to solve, i.e. greater than polynomial time for a solution. And some problems can't be decided in any amount of time, e.g. Halting problem. Here was a list of problems we came up with and their classification.

Easy - P	? - NP	Hard
Arithmetic	Traveling Salesman	Generalized Chess
Searching	Knapsack	Generalized Go
Sorting	Graph Coloring	Halting Problem
Shortest Path	3SAT	Finding all subsets of a set
Minimum Spanning Tree	K-Clique
Closest Pair	Prime Factoring
Convex Hull

On the other hand, problems in NP are ones that we can verify solutions to in polynomial time. Some of these problems are such that we don't know of a polynomial time solutions for these problems -- so they are not in P. However, we also don't know that no polynomial time solutions for them exist. So This is the basis of P vs. NP

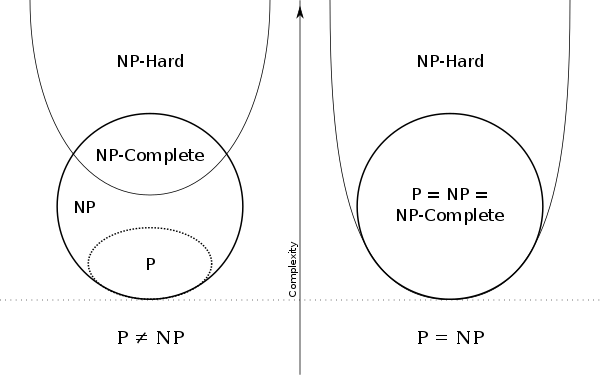
On this chart:

• P is the class of problems that are solvable in polynomial time.
• NP is the class of problems whose solutions are verifable in polynomial time (alternatively, they are solvable by a nondeterministic algorithm in polynomial time).
• NP-Complete is the class of hardest problems in NP.
• NP-Hard is the class of problems that are at least as hard as the hardest problems in NP.

Easiness and hardness here are relative terms on the amount of time it takes for an algorithm to compute a solution, i.e. its computational complexity.

P versus NP is one of the most important open questions in theoretical computer science. Its answer has many far reaching implications. For example, if P = NP, then problems such as prime factorization turn out to be computationally easy to solve. This would break public key cryptography as we know it. Public-key cryptography is widely used for secure data transmission over the internet.

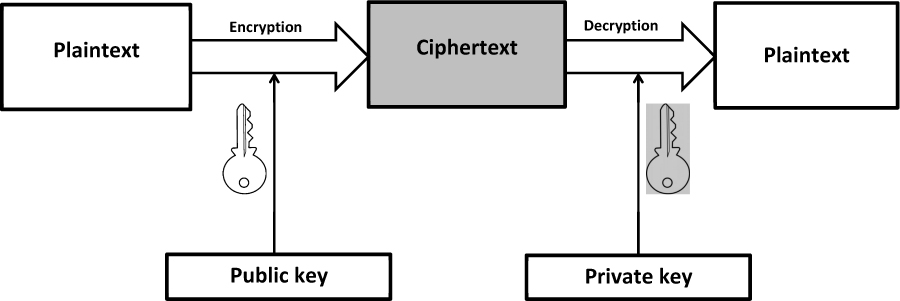
So we took a look at how public-key cryptography works in principle with a slightly simplified version of the RSA algorithm.

---

RSA Algorithm Basics

RSA is one of the first public-key cryptographic systems. The main idea is to use a public key to encrypt a message and a private key to decrypt.

Recall that it seemed to be much hard to factor a semiprime (a product of two primes) than it was to multiply two primes to find out what semiprime they compose. And around 2010, it took researchers 2 years to factor a 232 digit semiprime on a network of hundreds of computers.

$? \cdot ? = 91$ vs. $7 \cdot 13 = 91$

The rough idea is to use a large semiprime as your public key and the pair of primes that compose it as the private key. We can use an analogue to Fermat's Little Theorem to work this out. First, the Little Theorem:

Fermat's Little Theorem: If $N$ is prime, then $c^N \bmod N = c \bmod N$

For example: Let $N = 5$, then:
$1^5 \bmod 5 = 1$,
$2^5 \bmod 5 = 2$,
...,
$c^5 = c \bmod 5$

However, this gets us from $c$ back to $c$ in one step. We need a two step method so that we can encrypt in the first step and decrypt in the second.

Analogue Rule: If $N$ is a semiprime, then $N = p\cdot q$, where $p$ and $q$ are prime, and $c^{(p-1)(q-1)+1} \bmod N = c \bmod N$

For example, Let $N = 15$, then $p=3$, $q=5$, and $(p-1)(q-1)+1 = 9$:
$1^9 \bmod 15 = 1$,
$2^9 \bmod 15 = 2$,
...,
$c^9 \bmod 15 = c \bmod 15$

Encryption Scheme

For a given pair of primes $p$ and $q$, $(p-1)(q-1)+1$ will typically be a number that's not prime. So it can be represented as the product of two whole numbers, $r$ and $s$, (e.g.) $(p-1)(q-1)+1 = 9$ so $r = 3$ and $s = 3$. Raising a number to the power $(p-1)(q-1)+1$ can then be broken up into two steps, raising to the power of $r$, then raising to the power of $s$.

To encrypt a message, encoded as a number, pick two large primes $p$ and $q$, calculate the product $N$, and choose $r$ and $s$. Your public key is $r$ and $N$. Anyone can use these two numbers to encrypt a message to you. They raise their message to the $r^{th}$ power $\bmod N$ to generate the ciphertext.

Decryption Scheme

Your private key is $s$. To decrypt the encrypted message sent to you, you raise that ciphertext to the $s^{th}$ power $\bmod N$ to return to the plaintext.

If an adversary can compute what $p$ and $q$ are given $N$ (prime factorization problem), they can figure out what $s$ is and decrypt messages sent to you. Currently, we don't know of any quick way to factor large semiprimes. If P = NP, then prime factorization turns out to be an easy problem and anyone can quickly compute private keys.

This is a simplified version of the RSA encryption scheme. You can read more about the RSA algorithm at its wikipedia page RSA Algorithm

---

NP-Complete Problems and Polynomial-Time Reductions

We also looked at a class of problems called NP-complete problems. These are the hardest problems in NP. If we can find a way to solve any single one of NP-complete problems in polynomial time, then we've proven that P = NP. NP-Complete problems are defined as (1) being in the class NP and (2) everything in NP reduces to it in polynomial-time. Moreover, we can prove some candidate problem is in NP-Complete by (1) proving that it's in NP and (2) reducing an already known NP-Complete problem to the candidate. So we took a look at an example of a polynomial-time reduction: 3SAT to K-Clique.

Idea: If we have a black box that solves instances of problem X and we can use it to solve instances of problem Y, using a polynomial number of steps and a polynomial number of calls to the black box, then problem X is at least as hard as problem Y.

This is called a polynomial reduction of Y to X, written: $Y \leq_p X$.

Reduce 3SAT to K-Clique

3SAT - Determine whether a boolean formula in 3CNF can be satisfied
Literal: a boolean variable, e.g., $x$ or $\neg x$
Clause: a disjunction of literals, e.g., $x \lor y \lor z$
CNF: conjunctions of disjunctions, e.g., $(a \lor b) \land (\neg b \lor c) \land (b \lor c \lor d)$
3CNF: CNF where clauses are composed of exactly 3 literals, e.g. $(x \lor x \lor y) \land (\neg x \lor \neg y \lor \neg z)$

3SAT = {$\phi$ | $\phi$ is a satisfiable 3CNF}

K-Clique - Determine whether a graph has a k-clique
Clique: a subgraph in an undirected graph, where every pair of vertices is connected by an edge
K-clique: a clique containing k vertices

K-Clique = {$\langle G, k\rangle$| $G$ is an undirected graph with a k-clique}

Reduction of 3SAT to K-Clique

Idea: Convert 3CNF formulas to graphs in polynomial time. In the constructed graph, cliques of a specified size correspond to satisfying assignments of the 3CNF formula. So a solution for a k-clique problem can be directly used as a solution for the 3CNF problem.

Proof:

• Let $\phi = (a_1 \lor b_1 \lor c_1) \land (a_2 \lor b_2 \lor c_2) \land ... \land (a_k \lor b_k \lor c_k)$
• Reduce this 3CNF into an undirected graph $G$ by grouping the vertices of $G$ into $k$ groups of 3 vertices, each called a triple, $t_1, t_2, ..., t_k$
• Each triple corresponds to one of the clauses in $\phi$
  Each vertex in a triple corresponds to a literal in the corresponding clause
• Connect all vertices by an edge except the following:
  • vertices in the same triple
  • vertices representing complementary literals, e.g., $x$ and $\neg x$

Example:

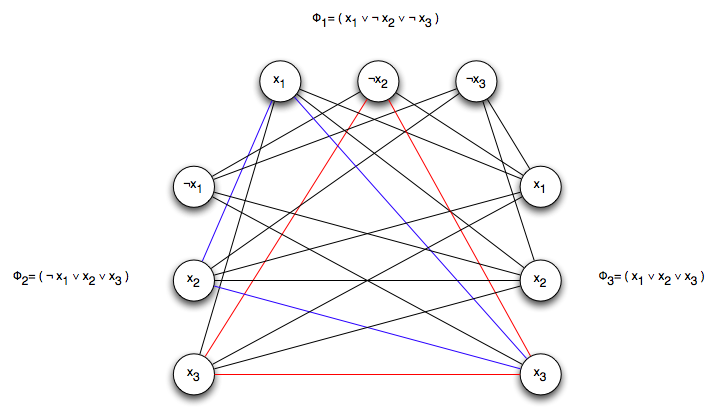
A 3CNF is satisfiable if and only if $G$ has a k-clique:
Suppose the 3CNF is satisfiable, then in the satisfying assignment, at least one literal in each clause is true. Each pair of those vertices must be connected, since we connect them all except complementary ones and ones within the same triple. Therefore $G$ contains a k-clique.

For the other direction, suppose that there exists a k-clique. Then, given the way we've constructed the graph, the vertices in the k-clique correspond to a satisfying assignment for the 3CNF.

Polynomial-time reduction

So we've reduced 3SAT to K-clique, i.e. 3SAT $\leq_p$ K-clique. In other words, we've transformed the input to our 3SAT problem into an input to the K-clique problem, solved K-clique, and transformed that solution back into a solution for 3SAT. Our transformation can be done in polynomial time, since on the length of the 3CNF, we initialize a vertex for each literal and at most we construct $|V|^2$ edges.

This means that K-clique is at least as hard as 3SAT. This shows that K-clique is NP-Hard, since we know that 3SAT is NP-complete. We further know that K-clique is in NP, since a solution is easy to verify. So K-clique is also NP-Complete. In general, we find new NP-Complete problems by reducing 3SAT or some other NP-complete problem to the new candidate and show that the candidate is in NP.