CS251 at CCUT Week 2: Propositional Logic

_{Image from "AN ACTUAL TEXTBOOK, AND: PHOTOS!" by Richard Zach is licensed under CC BY 4.0}

Another good logic textbook, Sets, Logic, Computation is an open source textbook which you can download at the Open Logic Project

---

During the first meeting, we talked a little bit about the background of logic and we looked at some arguments, identifying the premises and conclusions and translating them to Chinese.

Let's take a quick look at a couple more examples to warm up.

Examples:

• If Jupiter is more massive than Earth, then Jupiter has a stronger gravitational field than Earth. Jupiter is more massive than Earth. In conclusion, Jupiter has a stronger gravitational field than Earth.

• If we want to be safe, then we should have a state that can protect us. If we should have a state that can protect us, then we should give up some freedoms. Therefore, if we want to be safe, then we should give up some freedoms.

• Suppose $z \in X \cap (X \cup Y)$. Then $z \in X$, so $X \cap (X \cup Y) \subseteq X$. Next, Suppose $z \in X$. Then also $z \in X \cup Y$, and therefor also $z \in X \cap (X \cup Y)$. Thus, $X \subseteq X \cap (X \cup Y)$.

---

This week, we will begin to look at a language of logic, which we can use to represent arguments we find in English or Chinese and formally investigate their logical properties.

Outline:

• Language of Logic
• Syntax
• Semantics
• Atomic Sentences
• Compound Sentences
  • Not
  • And
  • Or
  • Conditional
• Exercises

A Language of Logic

A language of logic consists of a number of things:

1. A vocabulary of symbols used in the language.
2. A list or set of rules governing what strings of symbols (called formulas) are grammatically or syntactically well-formed in the language.
3. A semantics for the language, specifying the meanings for the symbols.

The Language

Because we always start discussing a logical system by discussing the language it uses, it is worth pausing to discuss the notion of using language to study language.

These comprise the first two parts of the logical system: a vocabulary and a syntax or grammar.

Metalanguage and Object Language

The languages of the systems we study are symbolic logical languages. They use symbols such as $\rightarrow$ and $\lor$, not found in ordinary English or Chinese.

However, we will talk and read about these logical languages in ordinary English or Chinese.

Whenever one language is used to discuss to study another, we can distinguish between the language that is being studied, called the object language, from the language in which we conduct the study, called the metalanguage.

What one is the object language and which one is the metalanguage for this course?

In this course, the object languages will be propositional logic (referred to as truth functional logic in the forallx textbook) and predicate calculus (referred to as first order logic in the textbook). In CS250, set theory was the main object language you studied.

Often we will use the metalanguage (English or Chinese or example) to prove things about the object language. Proving things already requires logical vocabulary! Fortunately English (and Chinese) has words like all, or, and, if, and so on. These are some of the logical vocabulary of English.

Propositional Logic

While I am here, we will study the Propositional Logic (PL) also called Truth Functional Logic (TFL) in the textbook. It's called the propositonal logic because the word 'proposition' means "sentence," and this is the logic of sentences.

Logical Vocabulary

The Propositional Logic, like any language contains a volcabulary. In this case, it is pretty small, so it is easy to study.

Logical Connectives: $\neg$, $\land$, $\lor$, $\rightarrow$, and $\leftrightarrow$

These are called, in order from left to right, "negation," "conjunction," "disjunction," "conditional," and "biconditional."

Atomic Sentences: Uppercase letters: A, B, C, ... P, Q, R

Sentence Schema (sentence variables): lowercase letters: $\textit{p, q, r}$

Parentheses: ( ), [ ], { }

Syntax

Propositional logic also has a syntax, rules that govern the structure of sentences in the language.

• Any atomic sentence, P, is syntactically well-formed.

• For any well-formed sentence, $p$, $\neg p$, is well-formed.

• For any well-formed sentence, $p$ and $r$, $(p \land r)$, $(p \lor r)$, $(p \rightarrow r)$, and $(p \leftrightarrow r)$ are well-formed.

Are the following sentences well-formed?

• $A \land B \to C$
• $\neg \neg C \lor B$
• $A \neg \to B$
• $A \land B \land C$
• $(A \land (B \lor C) \to D) \leftrightarrow (E \land F)$
• $(A \land (B \lor C) \to D) \leftrightarrow E \land F)$

Semantics and Principle of Bivalence

In studying languages, we often distinguish the syntax from the semantics of the language. The semantics of a language refers to the meanings.

In the propositional logic, the meaning of a sentence is its truth conditions. For this class, we will consider just two truth values: true and false. And we will assume the principle of bivalance

Principle of Bivalence: Each sentence of our language must be either true or false, not both, not neither.

So we will assume that each sentence is either true or false.

Back to Top

Atomic Sentences

CCUT is in Changchun.

This can be represented by a single capital letter, $A$. Atomic sentences are the basic building blocks of our language. Sentences are called atomic if they cannot be broken down into more basic parts.

In the propositional logic, sentences are either atomic or they are compound. Compound sentences are built up from sentences and the logical connectives mentioned above.

Compound Sentences

We have some idea of what the logical connectives mean, since we used English words to describe them. However, their precise meaning is given by a truth table.

A truth table is a table which represents all of the possible truth values a sentence of the propositional logic can take.

Here are the truth tables for our logical connectives:

p	q	p $\land$ q	p $\lor$ q	$\neg$p	p $\rightarrow$ q
T	T	T	T	F	T
T	F	F	T	F	F
F	T	F	T	T	T
F	F	F	F	T	T

These truth tables give the semantics for the logical connectives. Notice that these are lower case $p$ and $q$, indicating that these are sentence schema (or sentence variables).

Pattern Matching

So the compound sentence $A \rightarrow (B \lor C)$ has the form $p \rightarrow q$.

This type of pattern matching is important to understand.

Back to Top

"Not"

Not or negation is a unary connective. This means that it "connects" only to one sentence.

If $p$ is a well-formed sentence, then we can attach not to it: $\neg p$

The semantics for not are given by the following truth table:

p	$\neg p$
T	F
F	T

As we can see, negation gives us the opposite truth value of the original sentence.

"The Earth is not the center of the universe"

How do we translate this and what is the truth value?

Let R mean "The widget is replaceable."

1. The widget can be replaced.
2. The widget is irreplaceable.
3. The widget is not irreplaceable.

How should we translate these?

But be careful!

1. Jane is happy.
2. Jane is unhappy.

We might translate 1 to $H$, but 2 shouldn't be translated as $\neg H$. It may be that Jane is neither happy nor unhappy. The point here is that "Jane is not happy" does not necessarily mean the same thing as "Jane is unhappy."

Back to Top

"And" and "Conjunction"

I went to the party and I had fun.

p	q	p $\land$ q
T	T	T
T	F	F
F	T	F
F	F	F

Examples

1. Barbara is athletic and energetic.
2. Barbara and Adam are both athletic.
3. Although Barbara is energetic, she is not athletic.
4. Adam is athletic, but Barbara is more athletic than him.

Back to Top

"Or" and "Disjunction"

I go to the party or I study.

p	q	p $\lor$ q
T	T	T
T	F	T
F	T	T
F	F	F

Or is inclusive.

Examples

1. Either Faye will play videogames, or she will watch
   movies.
2. Either Faye or Ali will play videogames with me.
3. Either you will not have soup, or you will not have salad.
4. You will have neither soup nor salad.
5. You get either soup or salad, but not both.

Back to Top

"If... then..."

If I goto the party, then I will not study.

p	q	p $\rightarrow$ q
T	T	T
T	F	F
F	T	T
F	F	T

Examples

1. If Jean is in Paris, then Jean is in France.

2. Jean is in France only if Jean is in Paris.

3. For Jean to be in Paris, it is necessary that Jean be in France.

4. It is a necessary condition on Jean’s being in Paris that she
   be in France.

5. For Jean to be in France, it is sufficient that Jean be in Paris.

6. It is a sufficient condition on Jean’s being in France that she be in Paris

Do you understand the conditional?

Puzzle: Each card has a letter (consonant or vowel) on one side, and a number (odd or even) on the other.

Rule: If there's a vowel on one side of the card, there is always an odd number on the other.

Challenge: How many of the pictured cards must you turn over to see if any break this rule?

Back to Top

---

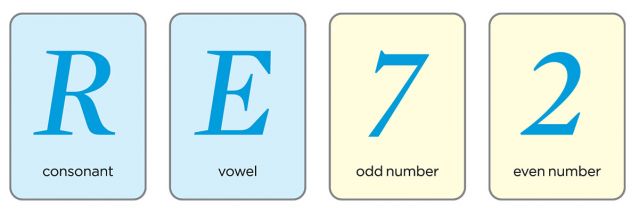
A Logic Puzzle

Four men and four women were nominated for two positions on the school board. One man and one woman were eleted to the positions. Suppose the men are named $A$, $B$, $C$, and $D$ and the women are named $E$, $F$, $G$, and $H$. Further, suppose that the following four statements are true:

• If neither $A$ nor $E$ won a position, then $G$ won a position.
• If neither $A$ nor $F$ won a position, then $B$ won a position.
• If neither $B$ nor $G$ won a position, then $C$ won a position.
• If neither $C$ nor $F$ won a position, then $E$ won a position.

Who were the two people elected to the school board?

Hint:

Let the capital $A$, $B$, $C$, and so on stand for the statements "$A$ was elected," "$B$ was elected, "$C$ was elected" and so on.

We know that one man and one woman were elected. In other words, we know that some long sentence of the form $(A \wedge E) \vee (A \wedge F) \vee (A \wedge G) \vee (A \wedge H) \vee (B \wedge E) \vee (B \wedge F) ...$ is true. In particular, we know that one of those disjuncts is true and the others are false.

We are given that (symbolizing 1-4 and finding some equivalences):

• $\neg (A \vee E) \rightarrow G \equiv A \vee E \vee G$
• $\neg (A \vee F) \rightarrow B \equiv A \vee F \vee B$
• $\neg (B \vee G) \rightarrow C \equiv B \vee G \vee C$
• $\neg (C \vee F) \rightarrow E \equiv C \vee F \vee E$

 
 
 
 
 
 
 
 
 
 
 
 
 

Solution:

So we can find the two people elected to the school board by determining which disjunct from our long sentence satisfies (or makes true) 1--4. Only $(B \wedge E)$ satisfies 1-4.

So $B$ and $E$ were the two people elected to the school board.

---

Exercises

Translations:

1. Mary is in Barcelona.
2. Those fruits are apples or they are not.
3. Those fruits are neither apples nor oranges.
4. If Professor Plum was murdered, then either Colonel Mustard or Mrs. White did it.
5. If you didn’t grow up speaking English it is difficult to understand many jokes made in English but, if you watch enough television, you can learn many of those jokes.

Answers
Back to Top

 
 
 
 
 
 
 
 
 
 
 
 
 

Answers

Back to Exercises

1. $M$
   $M$ is the atomic proposition "Mary is in Barcelona."

---

2. $A \lor \neg A$
   $A$ - "Those fruits are apples."

---

3. $\neg (A \lor O)$
   $A$ - "Those fruits are apples."
   $O$ - "Those fruits are oranges."

---

4. $P \rightarrow (M \lor W)$
   $P$ - "Professor Plum was murdered."
   $M$ - "Colonel Mustard did it."
   $W$ - "Mrs. White did it."

---

5. $(\neg G \rightarrow J) \land (W \rightarrow L)$
   $G$ - "You grew up speaking English."
   $J$ - "It is difficult to understand many jokes made in English."
   $W$ - "You watched enough TV."
   $L$ - "You can learn many English jokes."